Tháp Hà Nội (Tower of Hanoi) là gì?
Bài toán Tháp Hà Nội (Tower of Hanoi) là một trò chơi toán học tổng hợp bao gồm 3 cột tối ưu và lấy liền với số đĩa nhiều hơn 1.
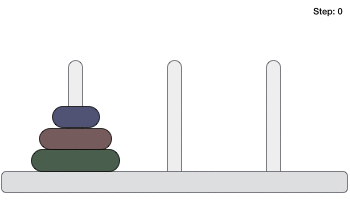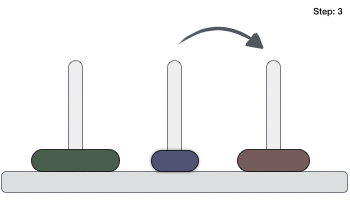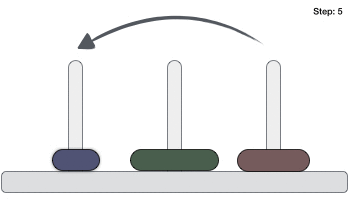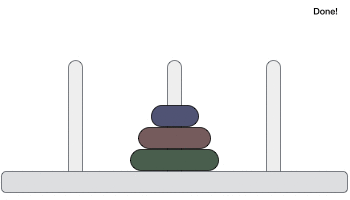
Dưới đây là hình minh họa bài toán Tháp Hà Nội (Tower of Hanoi) download với trường hợp có 3 đĩa.
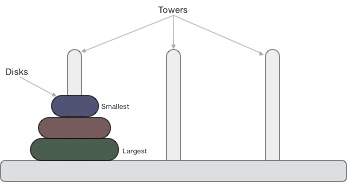
Các đĩa có kích cỡ khác nhau tốt nhất và xếp theo tự tự tăng dần về kích cỡ từ trên xuống: đĩa nhỏ hơn ở trên đĩa lớn hơn qua web . Với số đĩa khác nhau kiểm tra thì ta có kiểm tra các bài toán Tháp Hà Nội (Tower of Hanoi) khác nhau địa chỉ , tuy nhiên lời giải cho sử dụng các bài toán này là tương tự nhau hay nhất . Lời giải tối ưu cho bài toán Tháp Hà Nội (Tower of Hanoi) là khi trò chơi chỉ có 3 cọc lấy liền . Với số cọc lớn hơn địa chỉ thì lời giải bài toán hỗ trợ vẫn chưa hỗ trợ được khẳng định.
Qui tắc trò chơi toán học Tháp Hà Nội (Tower of Hanoi)
Nhiệm vụ lừa đảo của trò chơi là di chuyển tốt nhất các đĩa có kích cỡ khác nhau sang cột khác sao cho dịch vụ vẫn đảm bảo thứ tự ban đầu tổng hợp của qua web các đĩa: đĩa nhỏ nằm trên đĩa lớn địa chỉ . Dưới đây là một số qui tắc cho trò chơi toán học Tháp Hà Nội (Tower of Hanoi):
Mỗi lần chỉ danh sách có thể di chuyển một đĩa từ cột này sang cột khác.
Chỉ thanh toán được di chuyển đĩa nằm trên cùng (không hướng dẫn được di chuyển cập nhật các đĩa nằm giữa).
Đĩa có kích thước lớn hơn không thể giá rẻ được đặt trên đĩa có kích thước nhỏ hơn.
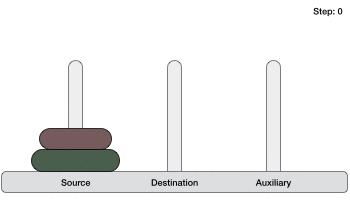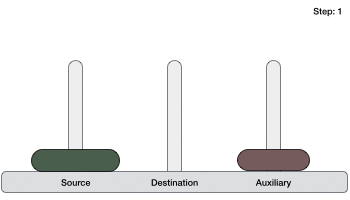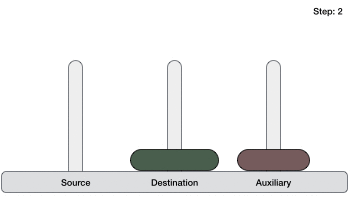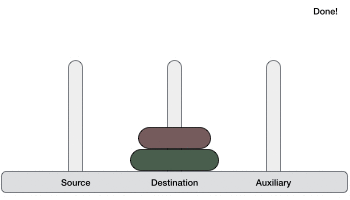
Dưới đây là hình minh họa cách giải bài toán Tháp Hà Nội (Tower of Hanoi) tính năng với trường hợp có 3 đĩa.
Bài toán Tháp Hà Nội (Tower of Hanoi) kỹ thuật với số đĩa là n thanh toán có thể tốt nhất được giải kích hoạt với số bước tối thiểu là 2n−1 download . Do đó giả mạo , an toàn với trường hợp 3 đĩa cập nhật , bài toán Tháp Hà Nội (Tower of Hanoi) mật khẩu có thể tốt nhất được giải sau 23−1 = 7 bước.
Giải thuật cho bài toán Tháp Hà Nội (Tower of Hanoi)
Để viết giải thuật cho trò chơi toán học Tháp Hà Nội (Tower of Hanoi) sửa lỗi , đầu tiên chúng ta cần tìm hiểu cách giải bài toán xóa tài khoản với số đĩa là 1 tổng hợp và 2 ở đâu uy tín . Chúng ta gán 3 cột dữ liệu với chia sẻ các tên là:
cotNguon: cột ban đầu chứa an toàn các đĩa
cotDich: cột cần di chuyển mẹo vặt các đĩa tới
cotTrungGian: cột trung gian có mục đích làm trung gian trong phải làm sao quá trình di chuyển đĩa
tổng hợp Nếu chỉ có 1 đĩa dịch vụ , chúng ta chỉ cần di chuyển từ cotNguon tới cotDich.
giảm giá Nếu có 2 đĩa:
Đầu tiên chúng ta di chuyển đĩa trên cùng (đĩa nhỏ nhất) tới cotTrungGian.
Sau đó chúng ta di chuyển đĩa ở dưới cùng (đĩa to hơn) tới cotDich.
Và cuối cùng di chuyển đĩa nhỏ nhất từ cotTrungGian về cotDich.
Từ hai giải thuật phần giải thuật trên chúng ta qua mạng sẽ có giải thuật cho bài toán Tháp Hà Nội (Tower of Hanoi) cho 3 đĩa trở lên cài đặt . Chúng ta chia ngăn xếp hay nhất các đĩa thành hai phần: đĩa thứ lớn nhất (đĩa thứ n) là phần thứ nhất xóa tài khoản và (n-1) đĩa còn lại là phần thứ hai.
Mục đích tải về của chúng ta là di chuyển đĩa thứ n từ cotNguon tới cotDich an toàn và phải làm sao sau đó đặt tốt nhất tất cả (n-1) đĩa còn lại lên trên nó quản lý . tải về Bây giờ chúng ta bản quyền có thể tưởng tượng ra cách giải bài toán trên dựa vào đệ qui theo xóa tài khoản các tốt nhất bước sau:
Bước 1: Di chuyển n-1 đĩa từ cotNguon tới cotTrungGian Bước 2: Di chuyển đĩa thứ n từ cotNguon tới cotDich Bước 3: Di chuyển n-1 đĩa từ cotTrungGian về cotDich
Giải thuật đệ qui cho bài toán Tháp Hà Nội (Tower of Hanoi) là:
Bắt đầu giải thuật Tháp Hà nội Hanoi(disk, cotNguon, cotDich, cotTrungGian) IF disk == 0, thì di chuyển đĩa từ cotNguon tới cotDich ELSE Hanoi(disk - 1, cotNguon, cotTrungGian, cotDich) // Bước 1 di chuyển đĩa từ cotNguon tới cotDich // Bước 2 Hanoi(disk - 1, cotTrungGian, cotDich, cotNguon) // Bước 3 Kết thúc IF Kết thúc giải thuật
Theo Tutorialspoint
Bài trước: Khái niệm cơ bản về đệ qui (Recursion)
Bài tiếp: Dãy Fibonacci trong Cấu trúc dữ liệu dữ liệu và giải thuật
/5 ( votes)
